An introduction to procedural lock and key dungeon generation

I’ve been down a bit of a rabbit hole regarding procedural generation lately. In particular, I’ve been studying techniques on lock and key dungeon generation, as it’s often called, though “dungeon” is a bit of a misnomer since most of these techniques can just as easily apply to other use cases. At its core, the lock and key model is about specifying paths of progression alongside the constraints to that progression. So while you absolutely can use it to generate a Zelda-like dungeon where you need to obtain keys or abilities to unlock new areas, you could also use it to model investigative games, where uncovering clues allows for new dialogue options that can affect the outcome of your mission, or use it to design an entire game world where each area, once completed, provides an item or triggers an event that lets you progress to the next one.

My research so far suggests that while this is an established type of content generation, the actual methodologies vary wildly and discussions on the subject can be somewhat limited and spread around the web. So today I’m going to provide an introduction to the concept of lock and key generation and demonstrate a basic implementation of it that can be used for any type of game. Let’s dive in.

Locks and keys

As mentioned previously, the concept behind lock and key generation is that there is a series of steps that must be taken in order to progress in the game. These steps can be entirely linear, ie you get a green key to open the green door which then let’s you get the red key to open the red door, or non-linear, such as requiring the player to complete four different tasks in any order before being able to progress the game further. There really aren’t any hard requirements about the composition of the game content at a high level, though you will want to refine the method for your particular use case, such as taking the spatial relationships and connectivity of rooms into account if trying to make a dungeon.

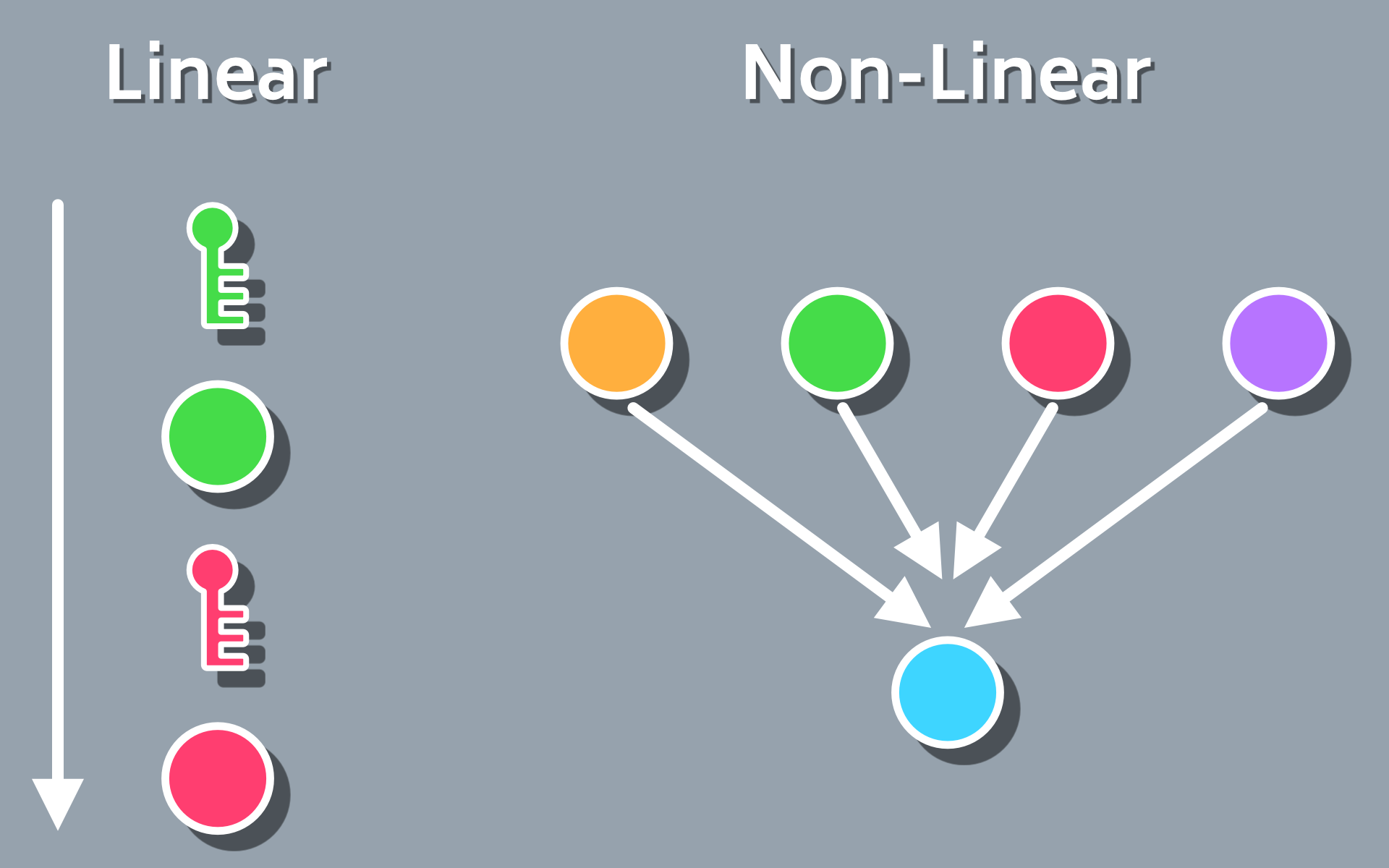
We can get more specific, though, based on our interests, and I would generally break down the types of locks into three categories:

• Big key locks
• Small key locks
• Stateful locks

Big keys

Big key locks are things like the boss key in a Legend of Zelda game, the boss itself in that and just about any other game, or an ability in a metroidvania. There is a lock that has one, and only one, way to open it. You cannot access a Legend of Zelda boss without the boss key, you can’t go onto the next dungeon without beating that boss (usually), and you can’t access a new area without the right ability or equipment.

These are the most common type of locks seen in video games, procedurally generated or not, since the vast majority of games have at least some hard requirements that must be completed in order to progress, even if it’s just completing the tutorial area. They’re also the easiest to generate since you just have to make sure the key, whatever it may actually be implemented as, comes before the lock. Doorway behind the boss is locked until it dies? Big key. Need to find a specific clue to confront the suspect? Big key. Even just a collection of levels in a puzzle game can be modeled as a very linear big key progression system.

Small keys

Taking things one step further, we can generalize our keys so that they work with multiple locks, but are consumed after use. I call this type of key a small key based on its usage in the Legend of Zelda series, where a single small key can be used to open one or more locks in a dungeon.

You can often open up the locks out of order from the required path of progression, but will eventually find more keys so that you can unlock other locks and get on the right path again. This type of semi-linearity is good, in my opinion, as it lets the player explore the dungeon how they wish and make mental notes of its layout while still keeping their options somewhat focused and allowing for the type of level design that linear gameplay offers.

For procedural generation, though, this method provides a non-trivial challenge: ensuring that the player always has access to enough keys so that they don’t get locked out of progressing because they opened the wrong lock. There may be a way to code this rule entirely at the time of generation that I’ve yet to discover, but otherwise it seems you need to pre-solve the dungeon after it’s generated and make sure this is always the case regardless of the path the player takes in the dungeon, making modifications to the dungeon if needed.

Stateful locks

The final type of lock and key combo, at least as I see it, is one that is stateful. Think of the water level in the Water Temple in Ocarina of Time or how games like Animal Crossing or Pokemon have items, events, and/or Pokemon that are only available at certain times of the day or even year.

These locks are complex enough to design by hand as it’s important to make sure the player doesn’t get stuck in an unsolvable situation no matter what path they take through the level. For procedural generation, the problem is amplified. To do it right, you’d most likely need to either drastically reduce the scope of these locks compared to a hand-designed game (which is reasonable), or use a solver to simulate all possible paths and make sure the player never gets stuck. Both methods are valid, they just might make your brain hurt if you try to get too complex too fast with them.

Generating a basic big key dungeon

And so finally, with the conceptual overview out of the way, how do we actually generate content based around this technique? That’s the million dollar question, and one that doesn’t have a simple answer as there’s no one generally accepted way to do it. Entire academic papers have been written proposing different methodologies, which is partially how I ended up down this rabbit hole to begin with. I’ll visit some of these techniques at some point in the future, but for today, and to keep things at an introductory level in line with the rest of this post, I’ll demonstrate a simple and approachable form of generation that I think will still be useful to a lot of people: tree-based big lock and key dungeons.

Hopefully it’s obvious why I’m sticking to big lock and key dungeons. By ignoring small and stateful locks, we can vastly simplify the requirements of the content generator since we just have to make sure we place a key somewhere in the dungeon before its matching lock. And keeping things tree-based makes creating this kind of dungeon super fast and easy to code. The caveat to this method is that since I’m keeping it extremely generic (so it can be used for any type of game and not just Zelda clones), it won’t tell you the exact layout of your dungeon if you’re using it for that purpose, only the order it should be traversed by the player. This could be seen as a bit of a benefit, though, since it means you can use any sort of dungeon generator you want as long as you can get that generator talking to this generator. This method can be expanded to do both, though, without too much effort and I’ll talk about that after I show the generic generator.

Methodology

So now let’s talk the algorithm, which is really simple. Here’s what we’ll do:

• Generate a list of nodes that serve as steps in the game’s progression
• Connect each node to a random node that comes before it in the list
• Place the key for that node in a random node that comes before it

And that’s it. From there, we can iterate on and configure the technique for whatever we want, but first let’s look at a bit of code, written in GDScript since I figure that’s what most of you are using if you’re on my site.

# Node is already used by Godot, so using an alternative name
class TreeNode:
	var children = []
	var id: int
	var keys = []
	
	func _init(node_id):
		id = node_id

var min_nodes = 7
var max_nodes = 14
var nodes = []

func generate() -> void:	
	var rand = RandomNumberGenerator.new()
	rand.randomize()

	nodes = []
	
	for i in range(rand.randi_range(min_nodes, max_nodes)):
		var new_node = TreeNode.new(i)
		
        # First node is the "entrance", so can't have a parent or a lock
		if i > 0:
			# Pick a random parent and key location from all nodes that came before it
			var parent = nodes[rand.randi_range(0, i - 1)]
			var key_location = nodes[rand.randi_range(0, i - 1)]
			
			parent.children.append(i)
			key_location.keys.append(i)
			
		nodes.append(new_node)

The TreeNode class is essentially just a data container to hold a reference to its children and the keys it holds. The id is there to make it easier to lookup later, but in this example the id is just the node’s placement in the nodes array and so is a bit redundant. The generate() function chooses how large of a tree to make (for i in range(rand.randi_range(min_nodes, max_nodes))) and then attaches each node to a random one that came before it before more or less repeating the process to place the key. By attaching nodes and keys this way, we can ensure that the player will always be able to access the key they need to progress.

Example outputs

Let’s look at a few examples of the dungeons this method creates. Also note that while I did add a graphical component to the code above on my end, it turns out that making an aesthetically pleasing n-ary tree (which is what this is) is way more complicated than generating one, so I’m redoing the output in Affinity Designer for presentation purposes.

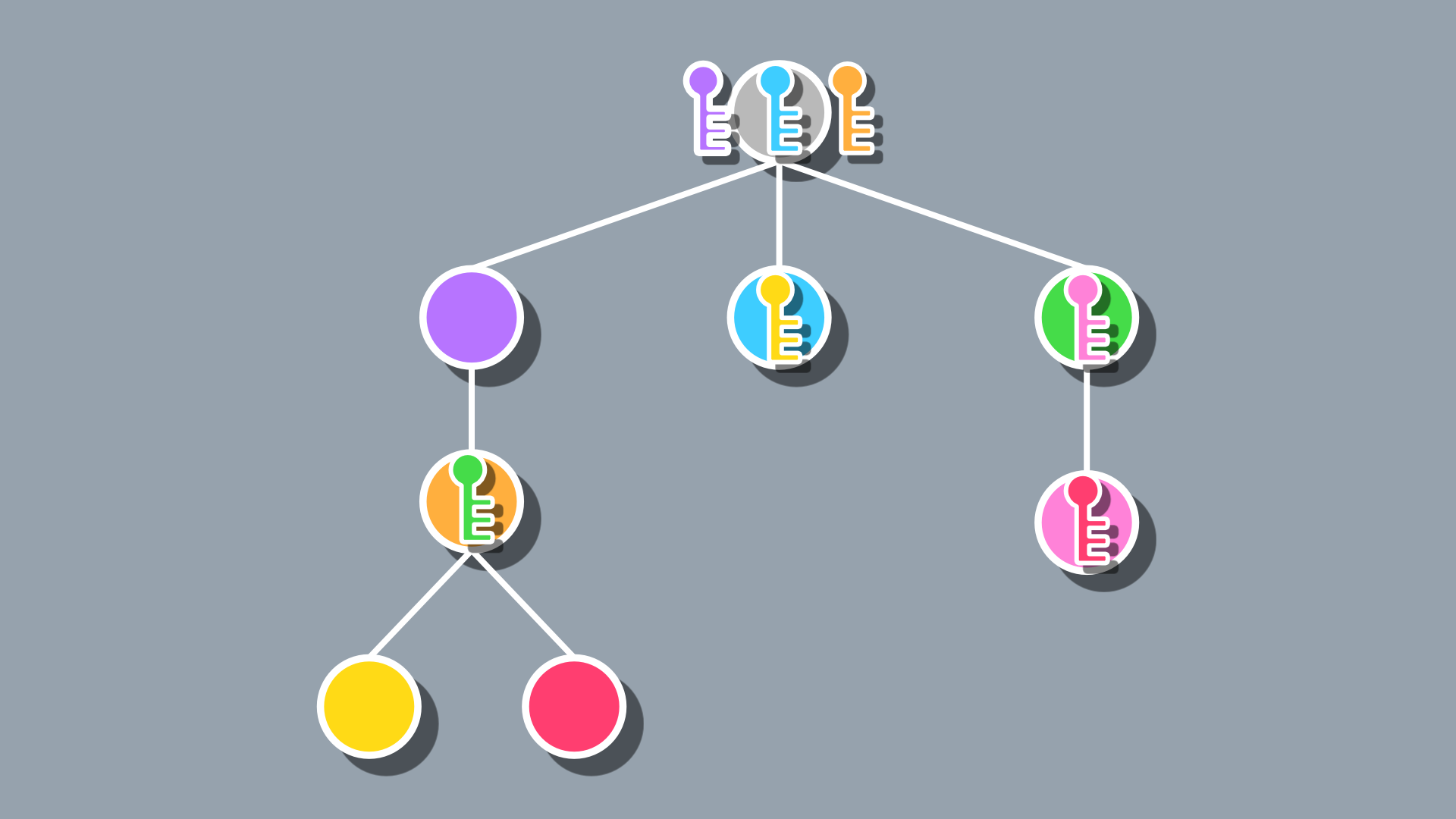
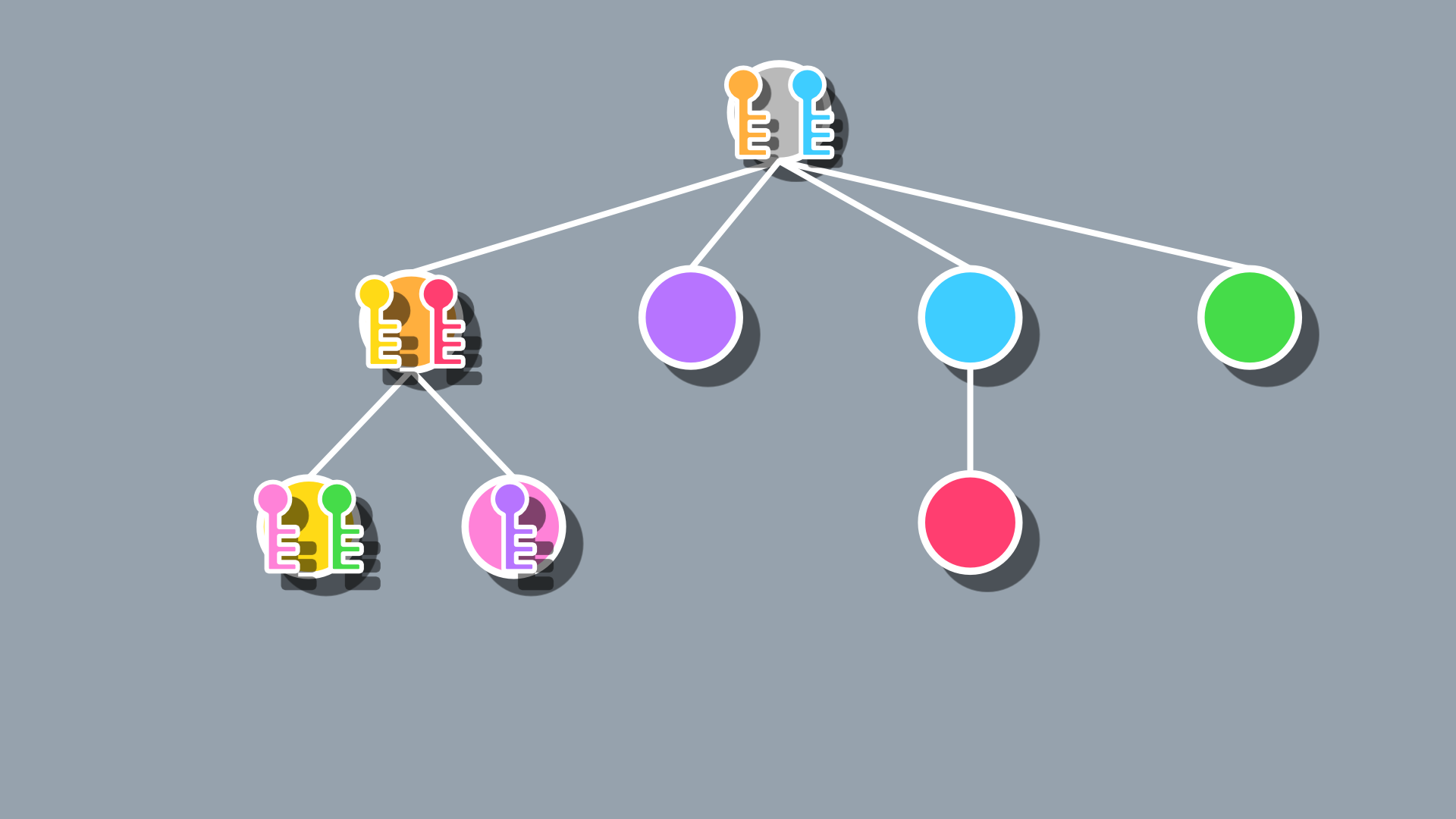
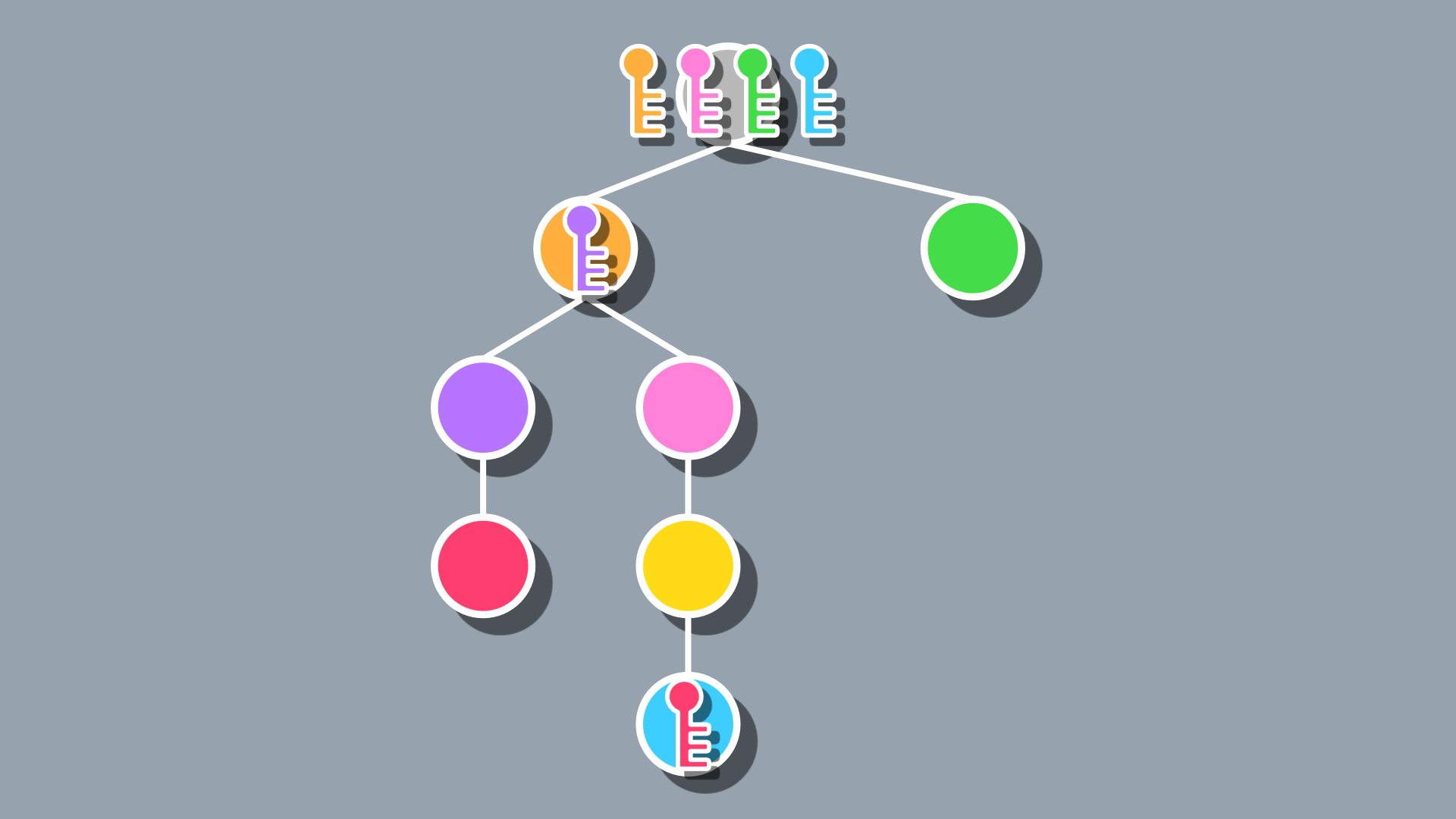
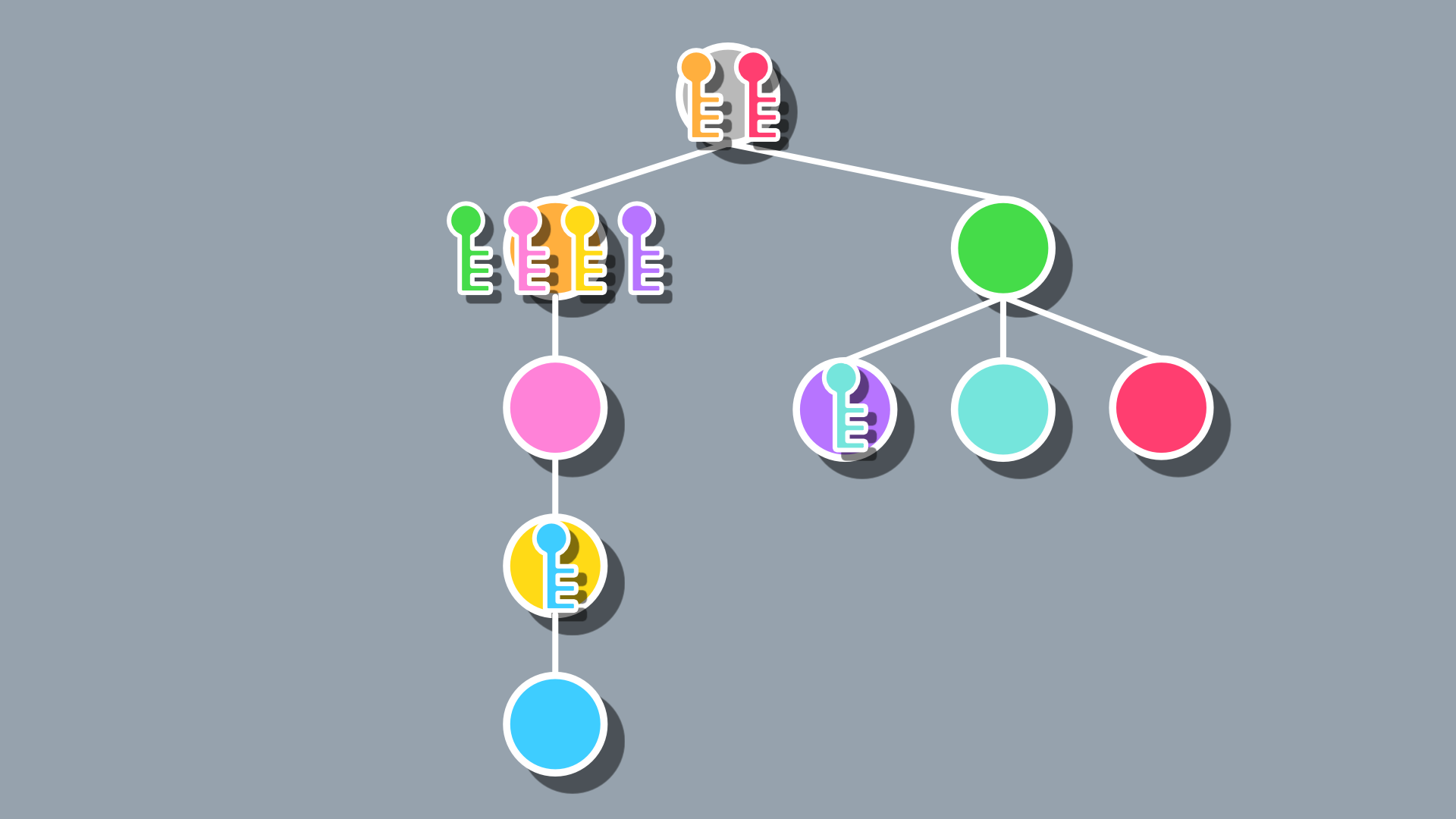
Overall, it’s not a bad first pass, as we do end up with progression paths that are unique from one another and non-linear, but there are some pretty obvious limitations. For one, we often end up with one or two nodes towards the beginning containing most keys for the dungeon. That combined with the fact that there are dead ends with no keys makes the non-linearity actually just feel tedious if the player chooses the wrong path. This method also encourages a lot of backtracking since the nodes can appear anywhere and often will appear far from their keys.

To fix the issue of key distribution, we can modify our code so that each node has a limit to how many keys it can hold, giving a much more balanced output by spreading the keys around more:

var max_keys_per_node = 2

func generate() -> void:	
	
    ...
	
	for i in range(rand.randi_range(min_nodes, max_nodes)):
		var new_node = TreeNode.new(i)
		
        # First node is the "entrance", so can't have a parent or a lock
		if i > 0:
			# Pick a random parent and key location from all nodes that came before it
			var parent = nodes[rand.randi_range(0, i - 1)]
			var key_location = select_key_location(i)
			
			...

func select_key_location(i: int) -> TreeNode:
    # Try to select a random node that doesn't have too many keys already
	var available_nodes = nodes.slice(0, i - 1)
	available_nodes.shuffle()
	
	for j in range(0, i - 1):
		var candidate = available_nodes[j]
		if candidate.keys.size() < max_keys_per_node:
			return candidate
	
    # If no suitable match found, return a random node that comes before the current one
	return nodes[rand.randi_range(0, i - 1)]

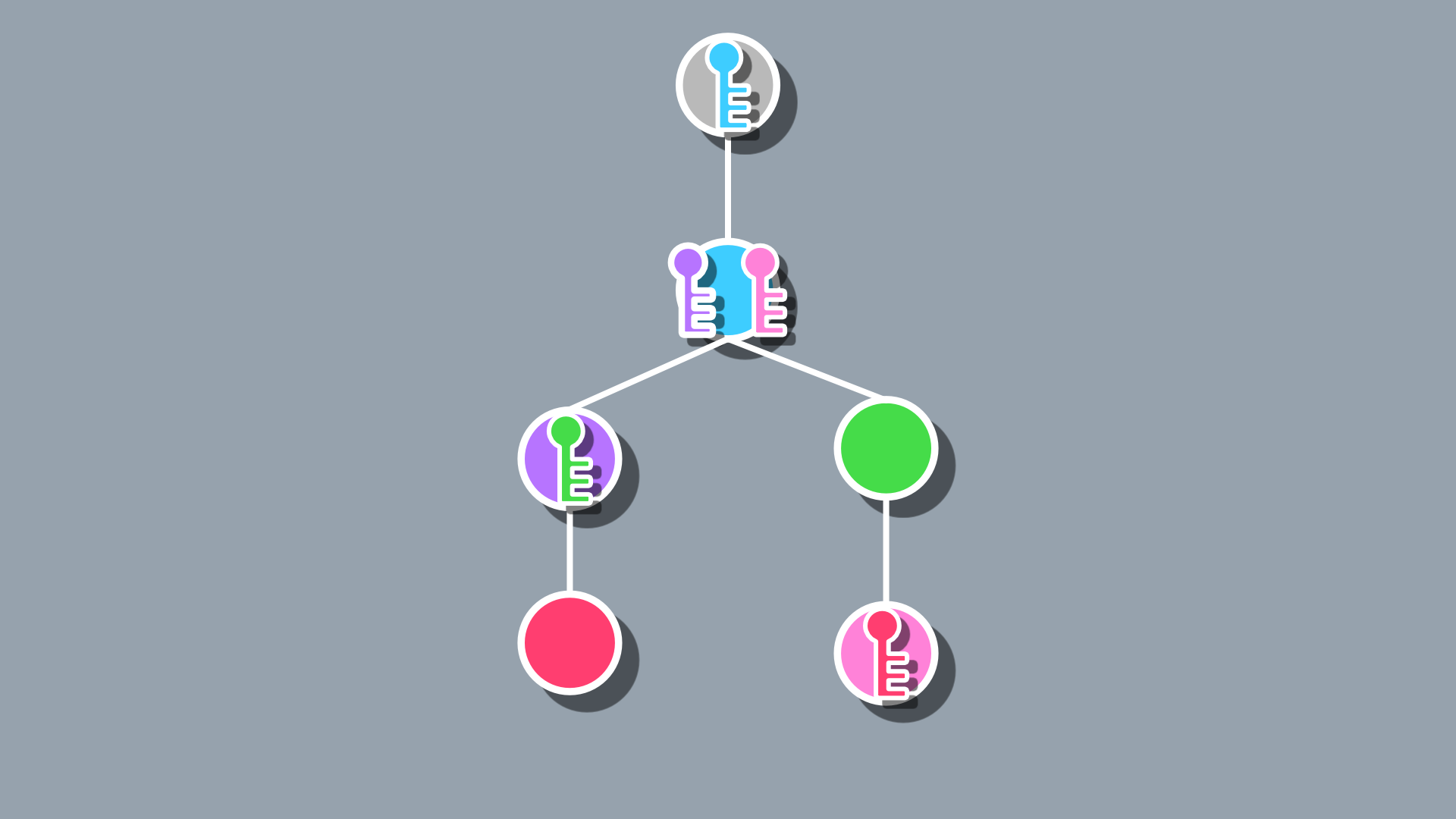
For the issue of dead-ends, it’s a bit harder to make a one-size-fits-all solution. I think in general, though, you should just make use the dead ends to offer valuable, but optional, items to encourage the player to explore. These end nodes are a great place to put valuable loot in a dungeon crawler, world-building information in a narrative game, etc. As long as each node can offer something of interest to the player, then it’s not necessarily a waste just because it doesn’t serve the main path to progression.

For the issue of backtracking, that once again is going to come down to your game, as it may not even really be an issue in a non-dungeon-based game. For dungeons, a shortcut to another part of the level could be added to some nodes to make things more interconnected. You could also bias the parent selection process to favor nodes close to where the key is placed so that the player is never too far from where they need to go. The technique for that is a bit beyond the scope of this post, but to point you in the right direction, if I were to go that route then I would use a distance formula to sort each potential parent based on distance from the key and shuffle a sub-selection, say those within 1 and 3 nodes of the key, to choose from (Googling “distance between nodes of an n-ary tree” is a good start if you’re curious).

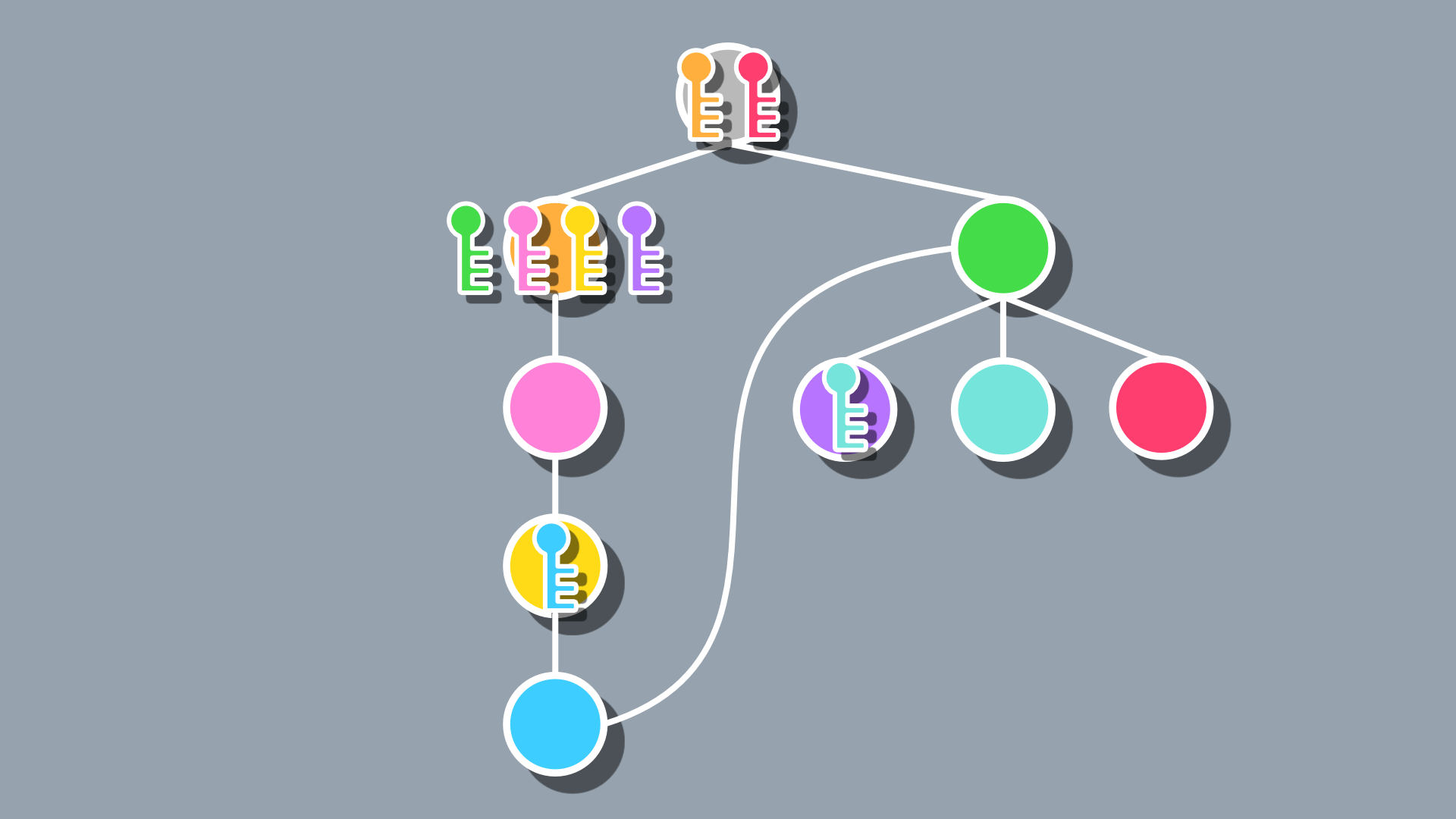
Incorporating spatial data

And now, let’s finally talk about how to make this method work specifically in a dungeon-generation context since the spatial relationship of nodes is important in that use case. I won’t be sharing code, though, as this post is already getting long (current read time says it’s the longest I’ve made), but hopefully there’s enough here to spark ideas and point you in the right direction. At a high level, there are three main ways I’d approach generating a dungeon spatially.

The first is to generate your dungeon using whatever means you prefer, and then group it to match the nodes generated via this method. This is the most flexible way to do it, but it does require analyzing and modifying the dungeon after it’s created to ensure it can be grouped according to the generated progression system, so could be a bit of a pain.

The next method is to use the nodes to represent regions of a dungeon and then generate mini-dungeons for each node. For instance, each node could represent a few rooms that you generate using your method of choice and then you connect them according to the generated tree. I like this method a lot as it gives you a lot of freedom with how you generate your levels but also lets the progression generator decide the general level layout for you and provides a decent integration of the two systems. This is the approach I would probably start with.

The final method would be to let the progression generator generate the entire level for you. This could be done by letting each node represent a room and then placing it on a grid, limiting connections to each node to only open grid spaces. With each node representing a room, you may decide you want more rooms and for not all of them to be locked. To do this, you could just place a few unlocked rooms in the tree after each locked one, essentially either duplicating or reusing, with a bit of modification, the main generate() function to create a sub-tree with the locked node as the root.

Conclusion

And that’s an introduction to lock-and-key dungeon generation. I recognize that there’s a lot I haven’t covered and that I did gloss over some details and ways of implementing what I discussed, but that’s because this is a pretty broad area of study with a lot of ways of tackling it, so there’s just no way to cover even a small fraction of it in one post. So I’m going to leave you with enough to get your feet wet for today, but I do intend to revisit this topic from time and time and hopefully share some more interesting techniques with you as I learn more about it myself.

Other resources

• The algorithm for Lenna’s Inception, named Metazelda, is an impressively advanced take on lock-and-key generation method and it’s worth checking if you want to see this method in use.
• This talk is a pretty interesting discussion on dungeon generation.
• Unexplored’s generation method is quite unique, focusing on cyclic graphs.